Understanding the Confusion Matrix in Machine Learning

Understanding the Confusion Matrix in Machine Learning

Introduction

In machine learning, classification models are commonly used to predict labels for data points. One of the most effective ways to evaluate the performance of a classification model is through a Confusion Matrix. The confusion matrix provides insight into not only the overall accuracy of the model but also the types of errors made. In this article, we will explain the confusion matrix in detail, discuss its significance, and provide a Python code example along with a visual representation.

What is a Confusion Matrix?

A confusion matrix is a table that summarizes the performance of a classification model. It compares the actual labels with the predicted labels generated by the model, helping us visualize how well the model is performing.

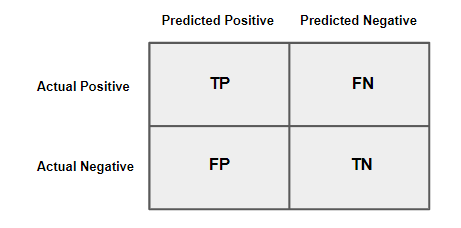
The confusion matrix is structured as a 2x2 (or larger) table for binary (or multiclass) classification tasks, where:

  • True Positive (TP): The model correctly predicted the positive class.
  • True Negative (TN): The model correctly predicted the negative class.
  • False Positive (FP): The model incorrectly predicted the positive class when it was actually negative (also known as a Type I error).
  • False Negative (FN): The model incorrectly predicted the negative class when it was actually positive (also known as a Type II error).

Confusion Matrix Structure (Binary Classification)

The confusion matrix for binary classification looks like this:

Each of these metrics can be used to calculate additional evaluation metrics like precision, recall, and accuracy.

Metrics Derived from the Confusion Matrix

Several key evaluation metrics can be calculated from the values in a confusion matrix. These include:

1. Accuracy

Accuracy measures the overall correctness of the model. It is defined as:

Accuracy = (TP + TN) / (TP + TN + FP + FN)

2. Precision

Precision measures how many of the positive predictions were correct. It is defined as:

Precision = TP / (TP + FP)

3. Recall (Sensitivity)

Recall measures how well the model identifies positive instances. It is defined as:

Recall = TP / (TP + FN)

4. F1-Score

The F1-Score is the harmonic mean of precision and recall, providing a balanced metric for imbalanced datasets. It is defined as:

F1-Score = 2 * (Precision * Recall) / (Precision + Recall)

Code Example

Below is a Python code example using the scikit-learn library to compute the confusion matrix, as well as precision, recall, and other metrics.

# Import necessary libraries
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
import seaborn as sns
import matplotlib.pyplot as plt

# Load a sample dataset
data = load_iris()
X = data.data
y = data.target

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Train a classifier
classifier = RandomForestClassifier()
classifier.fit(X_train, y_train)

# Make predictions
y_pred = classifier.predict(X_test)

# Compute confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)

# Display the confusion matrix
sns.heatmap(conf_matrix, annot=True, fmt="d", cmap="Blues", xticklabels=data.target_names, yticklabels=data.target_names)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()

# Classification report for precision, recall, and F1-score
print(classification_report(y_test, y_pred, target_names=data.target_names))

Confusion Matrix Output

Below is the output image of the confusion matrix generated from the code above:

Conclusion

The confusion matrix is a fundamental tool in machine learning that helps evaluate the performance of classification models. It provides detailed insights into the types of errors the model is making, and from the confusion matrix, other important metrics such as precision, recall, and F1-score can be calculated. Understanding and interpreting the confusion matrix is crucial to improving model performance and addressing any potential shortcomings in classification tasks.

Location: Pune, Maharashtra, India

Comments

Post a Comment

Popular posts from this blog

Comparison of CPU, GPU, APU and TPU

Comparison of CPU, GPU, APU, and TPU Introduction Modern computing devices utilize a variety of processing units to handle different types of tasks efficiently. The Central Processing Unit (CPU), Graphics Processing Unit (GPU), Accelerated Processing Unit (APU), and Tensor Processing Unit (TPU) each have unique strengths and are designed for specific applications. This article provides a detailed comparison of these processors, highlighting their characteristics and suitable use cases. Central Processing Unit (CPU) The CPU is the general-purpose processor that handles a wide range of tasks in a computer. It is designed for sequential processing and excels at performing complex calculations and logic operations. CPUs are found in virtually all computing devices, from desktops and laptops to servers and embedded systems. Use Cases Running operating systems and applications Performing general-purpose computing ...
Read more

Tensor Processing Unit (TPU): An In-Depth Overview

Tensor Processing Unit (TPU): An In-Depth Overview Introduction The Tensor Processing Unit (TPU) is a type of application-specific integrated circuit (ASIC) developed by Google specifically for accelerating machine learning tasks. TPUs are designed to handle the heavy computational demands of deep learning algorithms, providing high performance and efficiency for tasks such as neural network training and inference. By optimizing for tensor operations, which are fundamental to machine learning, TPUs offer significant advantages over traditional CPUs and GPUs in specific AI workloads. Historical Evolution Google introduced the first TPU in 2016 to address the growing computational requirements of its machine learning applications. The development of TPUs was driven by the need to improve the efficiency and speed of Google's AI services, such as search, translation, and image recognition. The first-generation TPUs were primarily desig...
Read more

Accelerated Processing Unit (APU): An In-Depth Overview

Accelerated Processing Unit (APU): An In-Depth Overview Introduction The Accelerated Processing Unit (APU) is a type of microprocessor that combines both the Central Processing Unit (CPU) and the Graphics Processing Unit (GPU) on a single chip. This integration aims to improve computing efficiency and performance, particularly for applications requiring both general-purpose processing and graphical computations. APUs are designed to offer a balance of power and efficiency, making them suitable for a wide range of devices from desktops to laptops and gaming consoles. Historical Evolution The concept of integrating a CPU and GPU on a single chip emerged as computing demands evolved. Early computing systems typically relied on separate CPUs and GPUs, leading to increased power consumption and space requirements. The idea of an APU was to streamline these components, enhancing performance and reducing energy usage. APUs were first introduc...
Read more